
Title
SMAC: Spatial Multi-category Angle-based Classifiers
Introduction
This is a novel Spatial Multi-category Angle-based Classifier (SMAC) for the efficient identification of neuroimaging biomarkers. The SMAC not only utilizes the spatial structure of high-dimensional imaging data, but also handles both binary and multi-category classiffication problems. This is a joint work with Prof. Hongtu Zhu and Prof. Yufeng Liu.Questions
1. Can we correctly classify the status of certain disease based on the voxel-wise imaging model?2. Can we improve the interpretability of the estimated models or coefficients?
Methods
Multi-category Angle-based Classifiers is a novel classification model proposed by Dr. Chong Zhang in 2014. It has very competitive performance in the multi-category classification problems. When applied in imaging data, we want to utilize the spatial structure of high-dimensional imaging data. Thus we add a generalized fused Lasso penalty to capture the spatial information of the imaging space. We apply the alternating direction method of multipliers (ADMM) to solve the optimization for our model. The ADMM is an algorithm that solves convex optimization problems by breaking them into smaller pieces, each of which are then easier to handle. Our package can be found at https://www.nitrc.org/.Findings
Our models can clearly identify the key discriminating region among different classes of noisy images. When applied in the Alzheimer's Disease Neuroimaging Initiative (ADNI) Magnetic resonance imaging (MRI) data, we can identify many key regions that have been proved to have significant correlation with the development of Alzheimer's disease.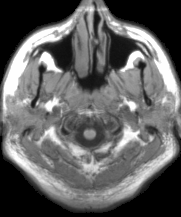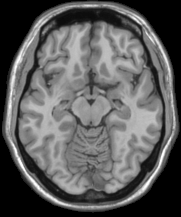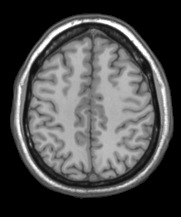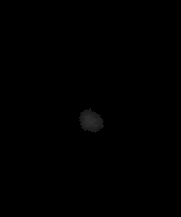
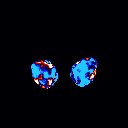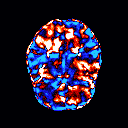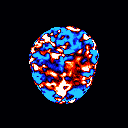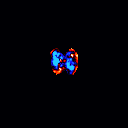

References
1. Chong Zhang and Yufeng Liu. Multicategory angle-based large-margin classification. Biometrika, 101(3):625-640, 2014.2. Tibshirani, Robert, et al. "Sparsity and smoothness via the fused lasso." Journal of the Royal Statistical Society: Series B (Statistical Methodology) 67.1 (2005): 91-108.
3. Boyd, Stephen, et al. "Distributed optimization and statistical learning via the alternating direction method of multipliers." Foundations and Trends® in Machine Learning 3.1 (2011): 1-122.