
Title
Tumor Heterogeneity: Clonal Structure Idetification
Introduction
Tumor at diagnosis consists of genotypically distinct cell populations referred to as (sub)clones which is often of crucial interest in cancer study. This is not only because the clonal structure itself provides an important clue for clinical treatment to the cancer but also subsequent analysis heavily depends on the identified structure.
Recently, PyClone was developped to efficiently identify the subclonal structure in DNA-seq. PyClone employs Bayesian hierarchical model based on
the so called cellular prevalence that measures proportions of cells harbouring a mutation. The structure is then identified by clustering the estimated
cellular prevalence under assumption of a perfect and persistent phylogeny of the clonal populations. The subclonal structure identification via PyClone
consists of two stages: i) estimating cellular prevalences and ii) clustering based on the estimated cellular prevalences.


Questions
Using low read depth whole genome sequencing data to identify clone and subclones in a tumor sample.Methods
a) We designed a pairwise difference penalized method, called CliP (Clonal structure identification through penalized pairwise difference), to try to address the problem
b) A non-concave penalty frame work was implemented to search for the most suitable solution
Findings
We have applied our method to the ICGC whole genome sequencing samples from different organ sites, obtained satisfactory results.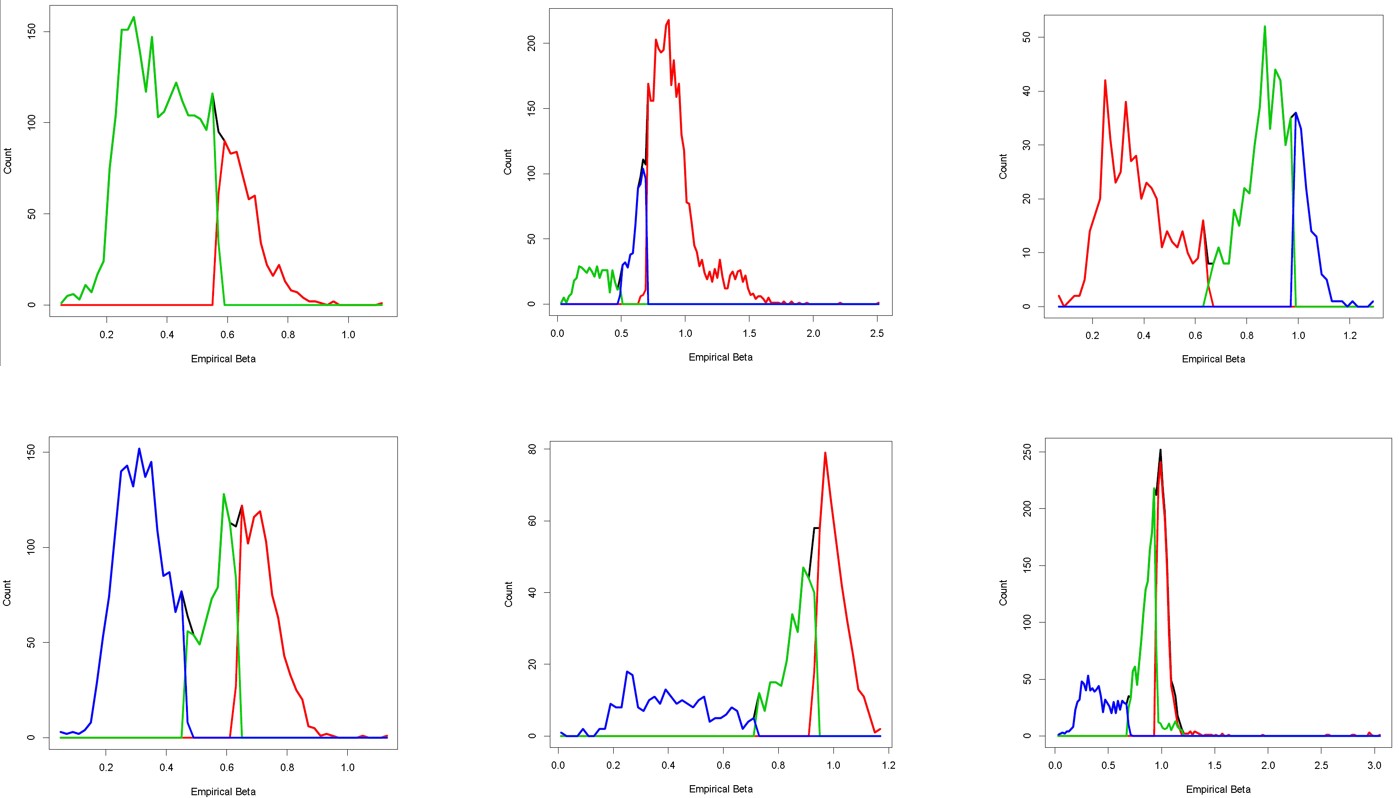
References
Fan, J. and Li, R. (2001). Variable selection via nonconcave penalized likelihood and its oracle properties, Journal of the American statistical Association 96(456): 1348-1360.
Ke, T., Fan, J. and Wu, Y. (2014). Homogeneity pursuit, Journal of the American Statistical Association .
Roth, A., Khattra, J., Yap, D., Wan, A., Laks, E., Biele, J., Ha, G., Aparicio, S., Bouchard-Cote, A. and Shah, S. P. (2014). Pyclone: statistical inference of clonal population structure in cancer, Nature methods .
Tibshirani, R., Saunders, M., Rosset, S., Zhu, J. and Knight, K. (2005). Sparsity and smoothness via the fused lasso, Journal of the Royal Statistical Society: Series B (Statistical Methodology) 67(1): 91-108.