Tutorial for running DeMixT and TmS
Wenyi Wang
In this tutorial, we use a subset of the bulk RNAseq data of prostate adenocarcinoma (PRAD) from TCGA (https://portal.gdc.cancer.gov/) as an example to demonstrate how to run DeMixT. The analysis pipeline consists of the following steps:
The analysis pipeline consists of the following steps:
- Obtaining raw read counts for the tumor and normal RNAseq data
- Loading libraries and data
- Data preprocessing
- Deconvolution using DeMixT
Obtain raw read counts for the tumor and normal RNAseq data
The raw read counts for the tumor and normal samples from TCGA PRAD are downloaded from TCGA data portal.
One can also generate the raw read counts from fastq or bam files by following the GDC mRNA Analysis Pipeline.
Load libraries and data
Load library
Load libraries and data
Load library
Load input data
Three data are included in the PRAD.RData.
PRAD: Read counts matrix (gene x sample) with genes as row names and sample ids as column names.Normal.id: TCGA ids of PRAD normal samples.Tumor.idTCGA ids of PRAD tumor samples.
A glimpse of PRAD:
Output:
TCGA-CH-5761-11A TCGA-CH-5767-11B TCGA-EJ-7115-11A TCGA-EJ-7123-11A TCGA-EJ-7125-11A
TSPAN6 3876 7095 5542 2747 8465
TNMD 14 51 13 24 63
DPM1 1162 2665 1544 1974 2984
SCYL3 777 1517 1096 1231 1514
C1orf112 136 343 214 280 339
FGR 230 511 263 755 262
Number of genes: 59427
Number of normal sample: 20
Number of tumor sample: 30 Data preprocessing
Conduct data cleaning and normalization before running DeMixT.
PRAD = PRAD[, c(Normal.id, Tumor.id)]
selected.genes = 9000
cutoff_normal_range = c(0.1, 1.0)
cutoff_tumor_range = c(0, 2.5)
cutoff_step = 0.1
preprocessed_data = DeMixT_preprocessing(PRAD,
Normal.id,
Tumor.id,
selected.genes,
cutoff_normal_range,
cutoff_tumor_range,
cutoff_step)
PRAD_filter = preprocessed_data$count.matrix
sd_cutoff_normal = preprocessed_data$sd_cutoff_normal
sd_cutoff_tumor = preprocessed_data$sd_cutoff_tumorData preprocessing
Conduct data cleaning and normalization before running DeMixT.
PRAD = PRAD[, c(Normal.id, Tumor.id)]
selected.genes = 9000
cutoff_normal_range = c(0.1, 1.0)
cutoff_tumor_range = c(0, 2.5)
cutoff_step = 0.1
preprocessed_data = DeMixT_preprocessing(PRAD,
Normal.id,
Tumor.id,
selected.genes,
cutoff_normal_range,
cutoff_tumor_range,
cutoff_step)
PRAD_filter = preprocessed_data$count.matrix
sd_cutoff_normal = preprocessed_data$sd_cutoff_normal
sd_cutoff_tumor = preprocessed_data$sd_cutoff_tumor
cat("Normal sd cutoff:", preprocessed_data$sd_cutoff_normal, "\n")
cat("Tumor sd cutoff:", preprocessed_data$sd_cutoff_tumor, "\n")
cat('Number of genes after filtering: ', dim(PRAD_filter)[1], '\n')Output:
The function DeMixT_preprocessing identifies two intervals based on the standard deviation of the log-transformed gene expression for normal and tumor samples, respectively, within the pre-defined ranges (cutoff_normal_range and cutoff_tumor_range).
In this example, we choose to select about 9000 genes before running DeMixT with the GS (Gene Selection) method to ensure that our model-based gene selection maintains good statistical properties.
DeMixT_preprocessing outputs a list object preprocessed_data containing:
preprocessed_data$count.matrix: Preprocesssed count matrixpreprocessed_data$sd_cutoff_normal: Actual cut-off value when desired genes are selected for normal samplespreprocessed_data$sd_cutoff_tumor: Actual cut-off value when desired genes are selected for tumor samples
Deconvolution using DeMixT
To optimize the parameters in
DeMixTfor input data, we recommend testing an array of combinations of number of spike-ins and number of selected genes.The number of CPU cores used by the
DeMixTfunction for parallel computing is specified by the parameternthread. By default,nthread = total_number_of_cores_on_the_machine - 1. Users can adjustnthreadto any number between 0 and the total number of cores available on the machine.For reference,
DeMixTtakes approximately 3-4 minutes to process the PRAD data in this tutorial for each parameter combination whennthreadis set to 55.
# Due to the random initial values and the spike-in samples used in the DeMixT function,
# we recommand that users set seeds to ensure reproducibility.
# This seed setting will be incorporated internally in DeMixT in the next update.
set.seed(1234)
data.Y = SummarizedExperiment(assays = list(counts = PRAD_filter[, Tumor.id]))
data.N1 <- SummarizedExperiment(assays = list(counts = PRAD_filter[, Normal.id]))
# In practice, we set the maximum number of spike-in as min(n/3, 200),
# where n is the number of samples.
nspikesin_list = c(0, 5, 10)
# One may set a wider range than provided below for studies other than TCGA.
ngene.selected_list = c(500, 1000, 1500, 2500)
for(nspikesin in nspikesin_list){
for(ngene.selected in ngene.selected_list){
name = paste("PRAD_demixt_GS_res_nspikesin", nspikesin, "ngene.selected",
ngene.selected, sep = "_");
name = paste(name, ".RData", sep = "");
res = DeMixT(data.Y = data.Y,
data.N1 = data.N1,
ngene.selected.for.pi = ngene.selected,
ngene.Profile.selected = ngene.selected,
filter.sd = 0.7, # We recommand to use upper bound of gene expression standard deviation
# for normal reference. i.e., preprocessed_data$sd_cutoff_normal[2]
gene.selection.method = "GS",
nspikein = nspikesin)
save(res, file = name)
}
}Note: We use a profiling likelihood-based method to select genes, during which we calculate confidence intervals for the model parameters using the inverse of the Hessian matrix. When the input data (e.g., gene expression levels from spatial transcriptomic data) is sparse, the Hessian matrix will contain infinite values, hence those confidence intervals can’t be calculated. In this case, gene selection will be performed through differential expression analysis (identical to DeMix_DE). This alternative is automatically performed inside DeMix_GS when the above situation happens.
PiT_GS_PRAD <- c()
row_names <- c()
for(nspikesin in nspikesin_list){
for(ngene.selected in ngene.selected_list){
name_simplify <- paste(nspikesin, ngene.selected, sep = "_")
row_names <- c(row_names, name_simplify)
name = paste("PRAD_demixt_GS_res_nspikesin", nspikesin,
"ngene.selected", ngene.selected, sep = "_");
name = paste(name, ".RData", sep = "")
load(name)
PiT_GS_PRAD <- cbind(PiT_GS_PRAD, res$pi[2, ])
}
}
colnames(PiT_GS_PRAD) <- row_namesThis step saves the deconvolution results (PiT) into a dataframe with columns named after the combination of the number of spike-ins and number of genes selected. Then one can calculate and plot the pairwise correlations of estimated tumor proportions across different parameter combinations as shown in the next slide.

Print out the average pairwise correlation of tumor proportions across different parameter combinations.
PiT_GS_PRAD <- as.data.frame(PiT_GS_PRAD)
Spearman_correlations <- list()
for(entry_1 in colnames(PiT_GS_PRAD)) {
cor.values <- c()
for (entry_2 in colnames(PiT_GS_PRAD)) {
if (entry_1 == entry_2)
next
cor.values <- c(cor.values,
cor(PiT_GS_PRAD[, entry_1],
PiT_GS_PRAD[, entry_2],
method = "spearman"))
}
Spearman_correlations[[entry_1]] <- mean(cor.values)
}
Spearman_correlations <- unlist(Spearman_correlations)
Spearman_correlations <- data.frame(num.spikein_num.selected.gene=names(Spearman_correlations), mean.correlation=Spearman_correlations)
Spearman_correlationsWe suggest selecting the optimal parameter combination that produces the highest average correlation of estimated tumor proportions.
Additionally, users are encouraged to evaluate the skewness of the PiT estimation distribution compared to a normal distribution centered around 0.5, as Significant skewness may indicate biased estimation.
We suggest selecting the optimal parameter combination that produces the highest average correlation of estimated tumor proportions.
Additionally, users are encouraged to evaluate the skewness of the PiT estimation distribution compared to a normal distribution centered around 0.5, as Significant skewness may indicate biased estimation.
Based on these criteria, spike-ins = 5 and number of selected genes = 1000 are identified as the optimal parameter combination. Using these parameters, we can obtain the corresponding tumor proportions.
data.frame(sample.id=Tumor.id, PiT=PiT_GS_PRAD[['5_1000']])
sample.id PiT
TCGA-2A-A8VL-01A 0.7596888
TCGA-2A-A8VO-01A 0.8421716
TCGA-2A-A8VT-01A 0.8662378
TCGA-2A-A8VV-01A 0.7616749
TCGA-2A-A8W1-01A 0.8291091
TCGA-2A-A8W3-01A 0.8159406
TCGA-CH-5737-01A 0.7314935
TCGA-CH-5738-01A 0.4614545
TCGA-CH-5739-01A 0.6349423
TCGA-CH-5740-01A 0.7095117 List the tumor specific expression
## Load the corresponding deconvolved gene expression
load("PRAD_demixt_GS_res_nspikesin_5_ngene.selected_1000.RData")
res$ExprT[1:5, 1:5]
TCGA-2A-A8VL-01A TCGA-2A-A8VO-01A TCGA-2A-A8VT-01A TCGA-2A-A8VV-01A TCGA-2A-A8W1-01A
DPM1 1710.194 1466.484 1680.4562 1644.944 1812.600
FUCA2 3782.990 4083.382 961.0578 4165.612 1896.901
GCLC 2382.106 1826.957 1527.4895 1409.707 1913.784
LAS1L 3329.766 2758.414 3520.9410 2834.415 2530.621
ENPP4 2099.591 3123.365 3173.3516 2856.371 7413.330Instead of selecting using the parameter combination with the highest correlation, one can also select the parameter combination that produces estimated tumor proportions that are most biologically meaningful.
Next,
We will provide a simple TmS tutorial which uses The estimated tumor-specific proportions (PiT) genertated from DeMixT. For more details, visit https://wwylab.github.io/TmS/articles/TmS.html.
TmS Calcualtion
Tumor-specific total mRNA expression (TmS) from bulk sequencing data, taking into account tumor transcript proportion, purity and ploidy, which are estimable through transcriptomic/genomic deconvolution.
TmS analysis pipeline consists of the following steps:
- Step 1: Estimate the proportion of total RNA expression (\(\pi\)) from tumor cells using RNAseq data.
- Achieved by using
DeMixT[1]
- Achieved by using
- Step 2: Estiamte the proportion of tumor cells and total copies of haploid genomes, i.e., tumor purity (𝜌) and tumor ploidy (\(\psi\)), using matched DNAseq or SNP array data.
- Step 3: Calculate TmS, the per cell haploid genome total RNA expression for tumor, using the estimated (\(\pi\)), (𝜌) and (\(\psi\)): \(TmS=[\pi (1-𝜌)2]/[(1-\pi)𝜌\psi]\).
Step 3: Calculate TmS using the estimated (\(\pi\)), (𝜌) and (\(\psi\)).
Consensus TmS estimation
For DNA-based deconvolution methods such as ASCAT and ABSOLUTE, there could be multiple tumor purity 𝜌 and ploidy \(\psi\) pairs that have similar likelihoods. Both ASCAT and ABSOLUTE can accurately estimate the product of purity 𝜌 and ploidy \(\psi\); however, they sometimes lack power to identify and separately. TmS is derived from the product of tumor ploidy and the odds of tumor purity. Hence, it is potentially more robust to ambiguity in the tumor purity and ploidy estimation, ensuring the robustness of the TmS calculation.
To calculate one final set of TmS values for a maximum number of samples, we use a consensus approach. We first calculate TmS values with tumor purity and ploidy estimates derived from both ABSOLUTE and ASCAT, and then fit a linear regression model on the log2-transformed \(TmS_{ASCAT}\) using the log2-transformed \(TmS_{ABSOLUTE}\) as a predictor variable. We remove samples with Cook’s distance ≥ 4/n and calculate the final
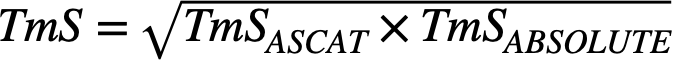
The agreement between the two methods in ploidy values was low in 20% of TCGA samples. However, a large portion of these samples showed consistency in the TmS values using either ASCAT and ABSOLUTE, reducing the number of filtered TCGA samples to ~5% (264 samples) [2]. This result supports the robustness of our consensus approach.
Input: Tumor-specific total mRNA proportions, tumor purities, tumor ploidies
Output: Consensus TmS
p: Tumor-specific total mRNA proportions estimated by DeMixTrho_ASCAT: tumor purity estimated by ASCATphi_ASCAT: tumor ploidy estimated by ASCATrho_ABSOLUTE: tumor purity estimated by ABSOLUTEphi_ABSOLUTE: tumor ploidy estimated by ABSOLUTE
TmS.calculate = function(p, rho, phi){
return(2 * p * (1 - rho) / (phi * rho * (1 - p)))
}
TmS.ASCAT = TmS.calculate(p, rho_ASCAT, phi_ASCAT)
TmS.ABSOLUTE = TmS.calculate(p, rho_ABSOLUTE, phi_ABSOLUTE)
TmS.df = data.frame(TmS.ASCAT.log2 = log2(TmS.ASCAT),
TmS.ABSOLUTE.log2 = log2(TmS.ABSOLUTE))
lm.fit = lm(TmS.df$TmS.ABSOLUTE.log2 ~ TmS.df$TmS.ASCAT.log2)
summary(lm.fit)
cooksd = cooks.distance(lm.fit)
cooksd.threshold = 4 / nrow(TmS.df)
cook.status = rep("Accept", nrow(TmS.df))
cook.status[cooksd > cooksd.threshold] = "Outlier"
TmS.df = TmS.df[cook.status == "Accept", ]
Consensus.TmS = sqrt(exp(TmS.df$TmS.ASCAT.log2)*exp(TmS.df$TmS.ABSOLUTE.log2))The estimated TmS values for TCGA PRAD tumor samples are shown in the violin plot below. 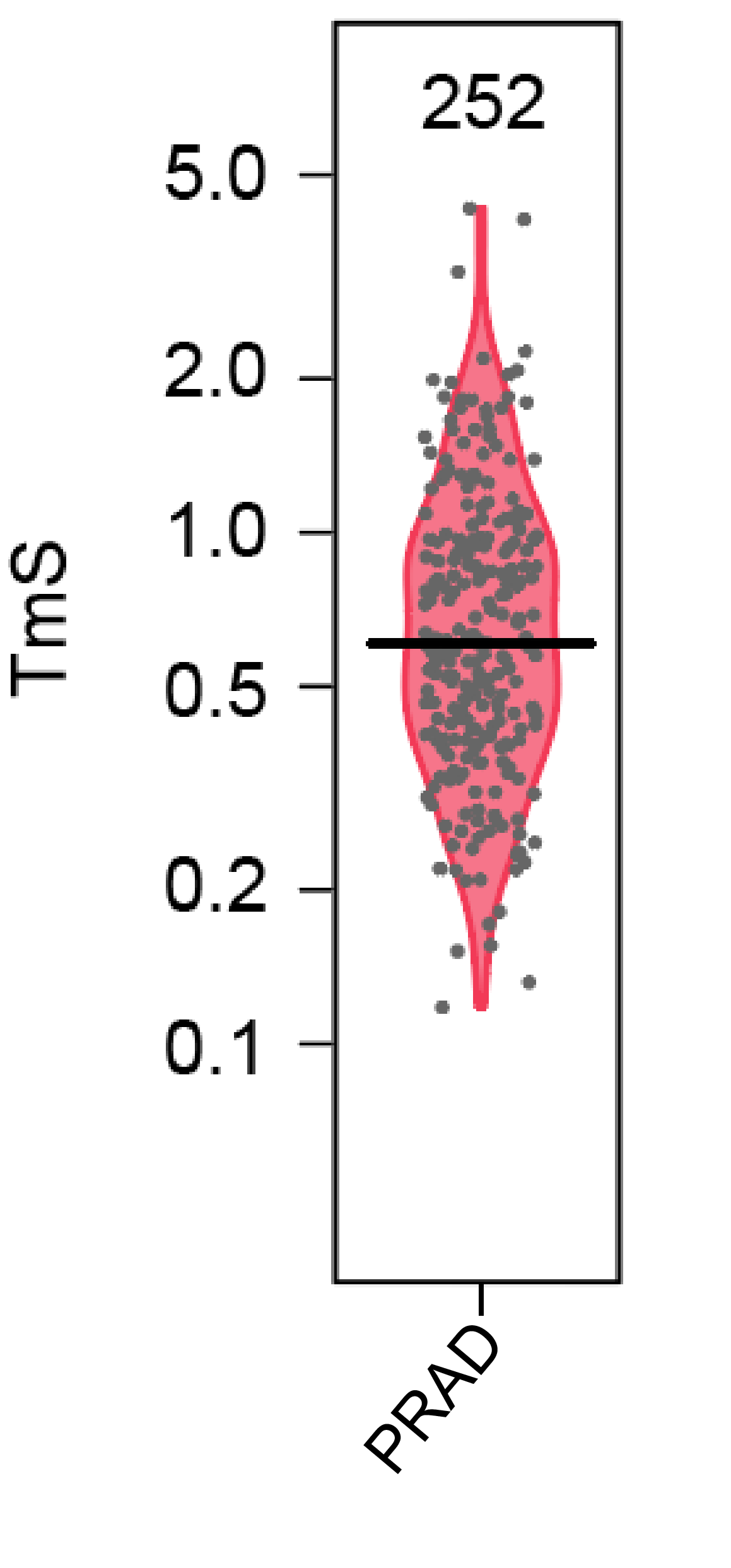
Reference
[1] https://github.com/wwylab/DeMixT
[2] Cao, S. et al. Estimation of tumor cell total mRNA expression in 15 cancer types predicts disease progression. Nat Biotechnol (2022). https://doi.org/10.1038/s41587-022-01342-x.
